Towards a theory of type structure

Thursday. November 25, 2021 - 8 mins

Reference: John C. Reynolds: Towards a theory of type structure. Symposium on Programming 1974: 408-423. paper

This paper (available at paper) introduces an extension of the typed lambda calculus which permits user-defined types and polymorphic functions.

The meaning of a syntactically valid program in a type-correct language should not depend on the representations used to implement its primitive types. In other words, types have the property of representation independence, which should hold for both user-defined types and primitive types. A user-defined type t should partition a program into an “outer” region in which t behaves like a primitive type and an “inner” region in which t is defined in terms of other types. The meaning of a program should remain the same if we change the representation of the type in the inner region and redefine the primitive operations consistently.

An extension of the typed lambda calculus

The author describes an extension of the typed lambda calculus which permits the binding of type variables. The author first considers a typed lambda which can deduce the type of every expression from the type of its free variables. For this purpose, it is sufficient to supply a type expression describing the variable at each point of variable binding.

\[ \lambda x \in t. x \]

denotes the identity function for objects of type t (the identity function in lambda calculus is \(\lambda x.x\)). The meaning of such expression depends on both free normal variables and the free type variables, which suggests the addition of a facility for binding type variables to create functions from types to values, called polymorphic functions.

\[ \Lambda t. \lambda x \in t. x \]

denotes the polymorphic identity function which maps t into the identity function for objects of type t.

Next, the author permits the application of polymorphic functions to type expressions, and introduces a new form of beta-reduction for such applications. In general, if r is a normal expression and w is a type expression, then

\[ (\Lambda t. r) [w] \]

denotes the application of the polymorphic function \(\Lambda t.r\) to the type w and is reducible to the expression obtained from r by replacing every free occurrence of t by w, after alpha-conversion.

Last, the author introduces a new kind of type expression to describe the types of polymorphic functions.

\[ \Delta t.w \]

denotes the type of polymorphic function which produces a value of type w when applied to the type t. If the expression r has type w, then the expression \(\Lambda t.r\) has type \(\Delta t.w\) (binding the occurrence of t in w). For example, the type of the polymorphic identity function is \(\Delta t. t \rightarrow t\).

Syntax

For sets \(S\) and \(S', S \times S'\) denotes the cartesian product of S and S’, \(S \Rightarrow S'\) denotes the set of functions from S to S’. When S and S’ are domains, \(S \rightarrow S'\) denotes the set of continuous functions from S to S’. If \(F\) is a function which maps each member of \(S\) into a set, we write \(\Pi_{x \in S} F(x)\) to denote the set of functions \(f\) such that the domain of \(f\) is \(S\) and \(\forall x \in S, f(x) \in F(x)\). For \(f \in S \Rightarrow S', x \in S, x' \in S'\), we write \([f | x| x']\) to denote the function \(\lambda y \in S.\)if \(y=x\) then \(x'\) else \(f(y)\).

Let T, V be two countably infinite sets: set T of type variables and set V of normal variables. The set of type expressions \(W\) is the minimal set satisfying:

• if \(t \in T\), then \(t \in W\)
• if \(w_1, w_2 \in W\), then \((w_1 \rightarrow w_2) \in W\)
• if \(t \in T, w \in W\), then \((\Delta t.w) \in W\)

Since \(\Delta t. w\) should bind the occurrences of t in w, one can define the notions of the \(free\) and \(bound\) occurrences of type variables and of alpha-conversion of type expressions directly. We write \(w \simeq w'\) to indicate w and w’ are alpha-convertible.

The author uses the notation

\[ w_1 |_t^{w_2} \]

to denote the type expression obtained from \(w_1\) by replacing every free occurrence of \(t\) by \(w_2\), after alpha-converting \(w_1\) so that no type variable occurs both bound in \(w_1\) and free in \(w_2\).

For normal expressions, we need to capture the idea that every normal expression has an explicit type. An assignment of a type expression to every normal variable which occurs free in a normal expression \(r\) must induce an assignment of a type expression to \(r\) itself which is unique (within alpha-conversion).

\(\forall Q \in V \Rightarrow W, w \in W, R_{QW}\) denotes the set of normal expressions for which the assignment of \(Q(x)\) to each normal variable \(x\) will induce the assignment of \(w\) to the normal expression itself.

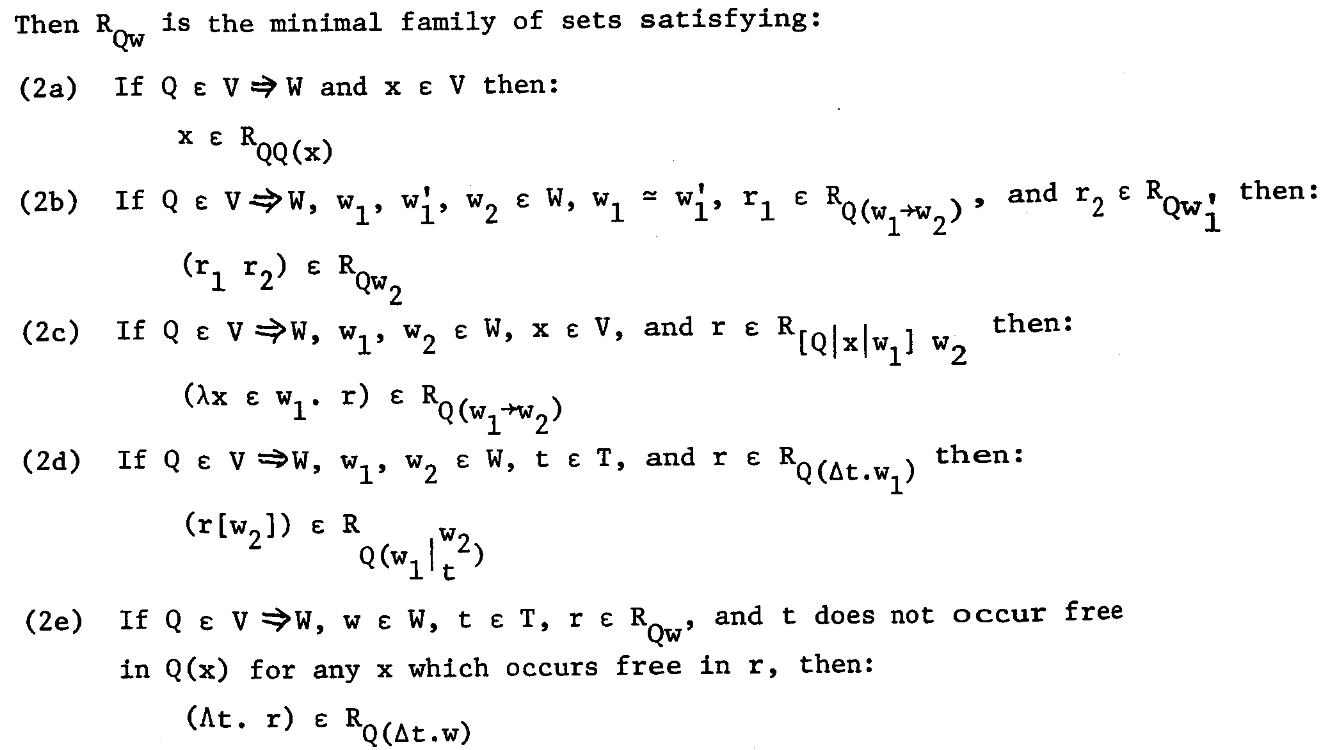
Conditions (2a) to (2d) concern normal variables, application, typed abstraction, and application for polymorphic functions. In (2e), the meaning of t in \(\Lambda t.r\) is distinct from its meaning in the surrounding context.

Semantics

The effect of a type expression is to produce a Scott domain, given an assignment of a domain to each free type variable occurring in the type expression. (As we will see later, this is actually flawed.) The meaning of a type expression \(B\) is given below, where \(W\) is the set of type expressions, \(\mathcal{D}\) is the class of all domains, and \(T\) is the set of type variables.

\[ B \in W \Rightarrow \mathcal{D}^T \Rightarrow \mathcal{D} \]

The effect of a normal expression is to produce a value, given an assignment of domains to its free type variables and an assignment of values to its free normal variables (an environment). This effect must conform to the type structure. For a type assignment \(\overline{D}\), a normal expression \(r \in R_{QW}\) must only accept environments which map each variable x into a member of the domain \(B[Q(x)](\overline{D})\), and r must produce a member of the domain \(B[w](\overline{D})\). For all \(Q \in V \Rightarrow W, w \in W\), meanings of normal expressions in \(R_{QW}\) is given below, where \(Env_Q(\overline{D}) = \Pi_{x \in V} B[Q(x)](\overline{D})\)

\[M_{QW}\in R_{QW}\Rightarrow \Pi_{\overline{D} \in \mathcal{D}^T}(Env_Q(\overline{D})\rightarrow B[w](\overline{D}))\]

Representations

The representation theorem in math states that every abstract structure with certain properties is isomorphic to another (abstract or concrete) structure wiki-rep. In this paper, the author defines the set of representations between \(D, D'\) as below, where \(I_D\) denotes the identity function on D.

\[rep(D, D') = \{<\phi, \psi> | \phi \in D \rightarrow D', \psi \in D' \rightarrow D, I_D \sqsubseteq \psi \circ \phi, \phi \circ \psi \sqsubseteq I_{D'} \}\]

For \(x \in D, x' \in D', \rho = <\phi, \psi> \in rep(D, D')\), we have \(\rho: x \mapsto x'\). x represents x’ according to \(\rho\) if and only if \(x \sqsubseteq \psi(x')\), equivalently, \(\phi(x) \sqsubseteq x'\).

We can extend it to all type variables. For \(\overline{D}, \overline{D'} \in \mathcal{D}^T\), we have

\[rep(\overline{D}, \overline{D'}) = \Pi_{t \in T} rep(\overline{D}(t), \overline{D'}(t))\]

Representation theorem

Let \(R_{QW}\) be the set of normal expressions, and suppose that \(\overline{D}, \overline{D'} \in \mathcal{D}^T, \overline{\rho} \in rep(\overline{D}, \overline{D'})\). For each type variable t, \(\overline{\rho}(t)\) is a representation between the domains \(\overline{D}(t), \overline{D'}(t)\). Suppose \(e, e'\) are environments such that for each normal variable x, e(x) represents e’(x) according to the relevant representation. Then we expect that the value of any \(r \in R_{QW}\) when evaluated with respect to \(\overline{D}\) and e should represent the value of the same normal expression when evaluated with respect to \(\overline{D'}, e'\), according to the relevant representation.

However, when choosing a representation, we assign a representation to every type variable, but not to every type expression. Intuitively, once we have chosen a representation for integer and real, this choice should also determine a representation for \(integer \rightarrow real\). In other words, the meaning of type expression maps an assignment of domains to type variables into a domain, and also maps an assignment of a representation into a representation.

Full semantics of type expressions

To extend the semantics function, the author noted that the combination of domains and representations forms a category, called category of types, denoted by \(\mathcal{C}\) (see wiki-category for what a category is). In this category, the set of objects is \(\mathcal{D}\), the set of morphisms from D to D’ is rep(D, D’). The composition is given by

\[<\phi', \psi'> \circ <\phi, \psi> = <\phi' \circ \psi, \psi \circ \phi>\]

and the identity for D is \(I_D = <I_D, I_D>\).

From the category of types, the author formed two more categories through standard constructions.

\(B[w]\) maps objects of \(C^T\) into the objects of C and morphisms of \(C^T\) into the morphisms of C.

Please refer to the paper paper for the definition of arrow and delta.