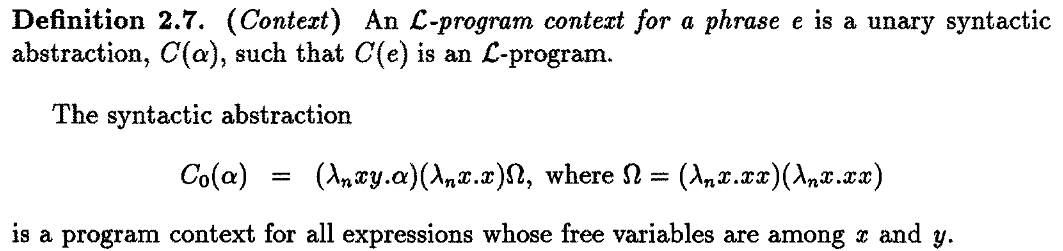On the expressive power of programming language

Saturday. April 16, 2022 - 3 mins

Reference: paper

How to compare different languages? This work attempts to develop a formal notion of expressiveness for programming languages.

The author started by inspecting some widely accepted examples of “syntactic sugar”. The informal approach suggests that a facility is expressible if every usage instance is replaceable by a behaviorally equivalent instantiation of an expression schema.

For example, consider a language with a while-loop construct but lacks a repeat-loop, then the repeat-loop is roughly equivalent to the while-construct. More precisely, for all statements s and expressions e

(repeat s until e) is expressible as (s; while (not e) do s)

When an instance of the expressed (left-hand) side is needed, the appropriate instantiation of the expressing (right-hand) side will perform the same operations.

In a dynamically-typed, functional language where procedures are first-class, then the lexical declaration of a variable binding in the form of a let-expression is an abbreviation of the immediate application of an anonymous procedure to the initial value

(let x be v in e) is expressible as (apply (procedure x e) v)

Functional languages can also realize the truth values through functional combinators

true is expressible as (procedure (x y) x) false is expressible as (procedure (x y) y)

The if-expression is similar to let-expression, but with some caveats.

(if tst thn els) is expressible as (apply tst thn els)

If the subexpression \(tst\) of an if-expression does not evaluate to a boolean value, a built-in if-construct may signal an error or diverge whereas the expressing phrases may return a proper value. The expressing phases may yield results in more situations than the built-in expressed constructs.

The essence of statements about “syntactic sugar” relationships can be summarized in a set of three formal properties.

• The expressing phrase is only constructed with facilities in a restricted sublanguage
• The expressing phrase is constructed without analysis of the subphrases of the expressed phrase
• Replacing the instances of an expressed phrase in a program by the corresponding instances of the expressing phrases has no effect on the behavior of terminating programs, but may transform a previously diverging program into a converging one.

The author then proposed a definition of the programming language.

A programming language \(L\) consists of

• a set of \(L\)-phrases, which is a set of freely generated abstract syntax trees (or terms), based on a possibly infinite number of function symbols \(F_1, F_2, \ldots\) with arity \(a, a_1, \ldots\).
• a set of \(L\)-programs, which is a non-empty subset of the set of phrases
• an operational semantics, which is a partial computable function, \(eval_L\), from the set of \(L\)-programs to an unspecified set of \(L\)-answers.

The function symbols, including the 0-ary symbols, are referred to as programming constructs or facilities. A syntactic abstraction is also known as derived operators, implemented as macros in Lisp. The precise definition is given in the paper.